Binary-Search

Jun 12, 2020

2 min read

Feb 8, 2025 12:42 UTC

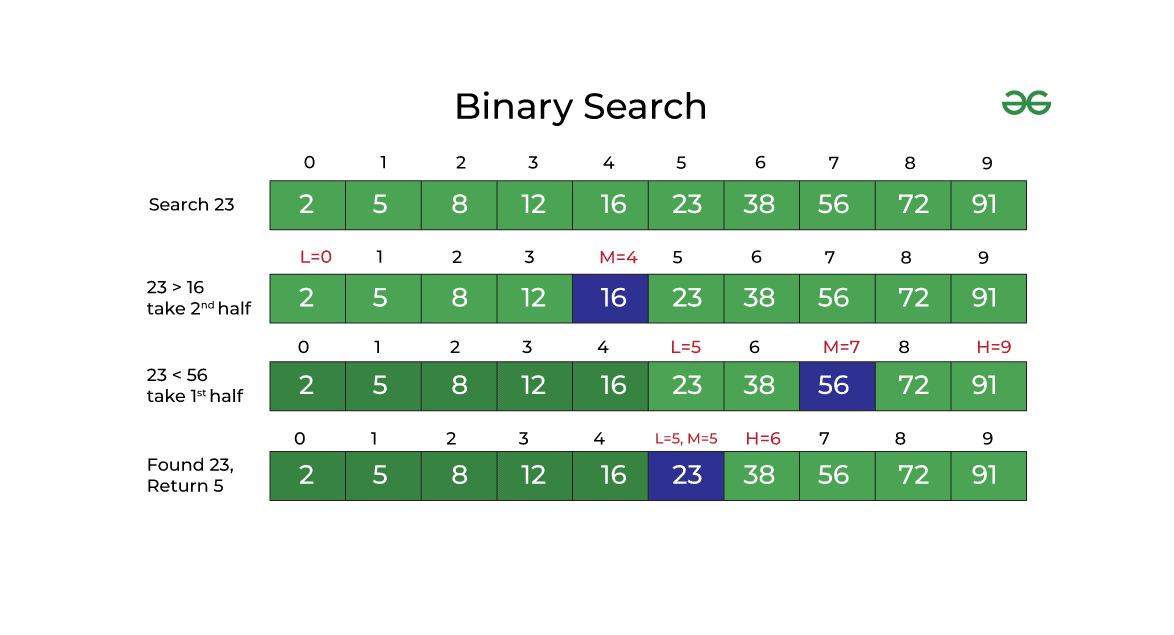
二分查找也称为折半查找（Binary Search），是一种效率较高的查找方法。它的一般查找过程为：首先，需要将待查的线性表按关键字排序，然后将表中间位置的元素的关键字与查找关键字比较。如果二者相等，则查找成功。如果不相等，则使用表的中间位置元素将表分为左右两个子表，查找关键字大于中间位置元素的关键字 -> 继续查询右子表；查找关键字小于中间元素的关键子 -> 继续查询左子表。重复以上过程直到查找到满足查询条件的元素，若最后细分到无法再划分子表时则没有此元素查询失败。由二分查找的原理我们很容易得出其时间复杂度为：lgN（以2为底）。

1. 基于有序数组的二分查找

想要在一个数组查找到一个元素的索引，最普通的方法就是将数组遍历一遍，将元素的关键字逐个的与查找关键字比较，直到找到元素返回其索引。这种方法的时间复杂度是线性级别的，在数组长度非常大且处于最坏的情况时，可能是无法解决的。而二分法就将解决这个这个问题的时间复杂度降低到了对数级别。如果数组长度为：100000000000, 在最坏的情况下，前者需要循环访问数组：1000亿次，而后者只需要访问数组约：36.5412次。这简直是降维打击，让我们能在有限算力的计算机上解决更多问题。下面是一个基于有序数组二分查找的实现。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
public class BinarySearch {
    //二分法查找元素的索引
    public static int Search(int[] a, int key){
        int lo=0, hi = a.length-1;
        while (lo <= hi){
            int mid = lo + (hi-lo)/2;
            if      (key > a[mid]) lo = mid + 1;
            else if (key < a[mid]) hi = mid - 1;
            //found
            else return mid;
        }
        //not found
        return -1;
    }
}

可以看到基于有序数组的二分查找实现非常简单，只需要两个辅助指针即可完成。

2.二分查找在实际问题中的应用

1.爱吃香蕉的珂珂(leetcode)

珂珂喜欢吃香蕉。这里有 N 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。

珂珂可以决定她吃香蕉的速度 K （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 K 根。如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）。

示例 1：

1
2
输入: piles = [3,6,7,11], H = 8
输出: 4

示例2：

1
2
输入: piles = [30,11,23,4,20], H = 5
输出: 30

也就是说珂珂想要慢慢的吃香蕉，但是又想把所有香蕉吃完，我们需要找到哪个满足这两个条件的最合适的速度K。

乍一看我们似乎无法将这个题目与二分查找关联起来。先抛开二分查找，我们快速的找一个简单暴力的方法：将所有可能的速度K都穷举一遍代入到问题中，最后求出最优解。K的范围的可能值显然为 [1, max(piles)]。最大的速度就是每次都可以将一堆香蕉吃完也就是max(piles)。

哦豁，现在是不是有点灵光乍现，这不就是和上面那个遍历有序数组差不多吗？这时投入我们的二分查找优化算法，减少访问数组的次数,提升效率。具体解题如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public int minEatingSpeed(int[] piles, int H) {
        int left = 1, right = getMax(piles);
        while(left <= right){
            int mid = left + (right - left)/2;
            if(canEatAll(piles, mid, H)){
                //能吃完(查询到)
                right = mid - 1;
            }else{
                //不能吃完
                left = mid + 1;
            }
        }
        return left;
    }

    //判断在当前速度k下，珂珂能否吃完所有香蕉
    boolean canEatAll(int[] piles, int k, int H){
        int time = 0;
        for(int n : piles){
            time += timeOf(n, k); 
        }
        return time <= H;
    }

    //给定速度k下，吃完数量n香蕉的时间
    int timeOf(int n, int k){
        return (n/k) + ((n % k > 0) ? 1 : 0);
    }

    //香蕉最多的堆的香蕉数
    int getMax(int[] piles){
        int max = 0;
        for(int n : piles){
            max = Math.max(n, max);
        }
        return max;
    }
}

这里的解题中二分查找的使用和上面一般的实现有一些区别，一般实现是默认数组元素不重复的，如果找到元素后就立即返回元素的索引。而这里珂珂吃香蕉，只要是大于等于答案速度的取值都可以让珂珂把香蕉吃完，也就相当于有许多满足查询条件的元素，也就相当于是元素重复了。

而我们的珂珂想要慢慢的吃，也就是要满足条件的速度中最慢的那一个取值。所以我们需要找到满足条件最靠左的速度。所以在满足能吃完的条件时我们不能直接返回速度，而是将其左边子数组的最大索引赋值给右指针。然后在指针值不满足循环条件时返回左指针的值，也就是最慢能吃完香蕉的速度。

图片资料来自：

Algorithms (4th Edition)
GeeksforGeeks

Jun 14	Binary-Search-Tree	3 min read
Jul 06	Hash-Table	5 min read
Jun 14	Red-Black-BST	4 min read
Jul 24	Shortest-Path	9 min read
Jul 21	Minimum-Spanning-Tree	7 min read