有向图中的有向是指图中每一条边都是有向的,每一条边连接的两个顶点都是一个有序对,它们的邻接性是单向的。能从 v->w ,不一定能从 w->v。这是有向图与无向图的本质区别,这种区别导致了两种图处理算法上的巨大差异。
1. 术语表 学习有向图的处理算法我们,需要了解一些定义和术语。如下表:
术语 条件(释义) 有向图 一幅有方向性的图,由一组顶点和一组有方向的边组成,每条有方向的边都连接着有序的一对顶点。 出度 顶点指出边的总数 入度 指向该顶点边的总数 有向路径 由一系列顶点组成,对于其中的每一个顶点都存在一条有向边从它指向序列中的下一个顶点 有向环 至少含有一条边且起点终点相同的有向路径 简单有向环 是一条不含有重复顶点的环(除起点和终点相同) 长度(路径,环) (路径,环)所包含的边数 有向无环图(DAG) 不含环的有向图 强连通 有向图中的两顶点相互可达,称两顶点强连通。如果有向图所有顶点强连通则图强连通
2. 有向图数据类型 有向图虽然在逻辑上比无向图中多出了许多限定条件,但是其数据类型的实现更简单。由于边是有向的,所以我们用邻接表表示边时,只会出现一次。具体实现细节如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
public class Digraph {
private final int V ; // 顶点数
private int E ; // 边数
private Node [] adj ; // 邻接表
/**
* 邻接表结点静态内部类
*/
private static class Node {
int vertex ; // 顶点
Node next ; // 下一个元素的引用
Node (){}
Node ( int vertex , Node next ){
this . vertex = vertex ;
this . next = next ;
}
}
public Digraph ( int V ){
this . V = V ;
this . E = 0 ;
this . adj = new Node [ V ]; // 创建邻接表
}
public Digraph ( BufferedReader reader ) throws IOException {
this ( Integer . parseInt ( reader . readLine ())); // 读取 V
int E = Integer . parseInt ( reader . readLine ()); // 读取 E
for ( int i = 0 ; i < E ; i ++){
String str = reader . readLine ();
String [] edge = str . split ( " " );
int v = Integer . parseInt ( edge [ 0 ]);
int w = Integer . parseInt ( edge [ 1 ]);
addEdge ( v , w ); // 添加边
}
}
/**
* 添加一条边 v -> w
* @param v 顶点1
* @param w 顶点2
*/
public void addEdge ( int v , int w ){
Node first = adj [ v ];
adj [ v ] = new Node ( w , first ); // 将顶点w添加到顶点v的链表中
E ++;
}
/**
* 获取与顶点 v 邻接的所有顶点
* @param v 顶点
* @return 邻接顶点set集合
*/
public Set < Integer > adj ( int v ){
Node node = adj [ v ];
Set < Integer > set = new HashSet <>();
while ( node != null ){
set . add ( node . vertex );
node = node . next ;
}
return set ;
}
/**
* 获取当前图的反向图
* @return 反向图
*/
public Digraph reverse (){
Digraph dr = new Digraph ( V );
for ( int v = 0 ; v < V ; v ++){
for ( int w : adj ( v ))
dr . addEdge ( w , v );
}
return dr ;
}
public int V (){ return V ;}
public int E (){ return E ;}
上述实现与 Graph 无向图数据类型的实现基本相同,更改了addEdge() 方法,只插入一个结点。增加了一个 reverse() 方法返回图的反向图(将所有边的方向反转)。
3. 有向图中的可达性 能使用一种算法判断有向图中的两个顶点间是否存在一条有向路径是一个非常切实的需求,因为图只要稍微一复杂凭肉眼就很难判断顶点是否可达另一顶点。
这个问题又叫做:点单可达性 (给定一幅有向图和一个起点 s,“是否存在一条从 s 到达给定顶点 v 的有向路径?”)解决这个有向图的问题我们只需要将 DepthFirstSearch 稍作改动,将 Graph 数据类型替换位 Digraph 数据类型即可。DirectedDFS具体实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class DirectedDFS {
private boolean [] marked ; // 标记已访问过的顶点
private int count ; // 与起点连通的结点数
public DirectedDFS ( Digraph g , int s ){
marked = new boolean [ g . V ()];
dfs ( g , s );
}
public DirectedDFS ( Digraph g , Iterable < Integer > sources ){
marked = new boolean [ g . V ()];
for ( int s : sources )
if (! marked [ s ]) dfs ( g , s );
}
/**
* 深度优先搜索函数
* @param g 图
* @param v 当前顶点
*/
private void dfs ( Digraph g , int v ){
marked [ v ] = true ;
count ++;
for ( int w : g . adj ( v ))
if (! marked [ w ]) dfs ( g , w );
}
/**
* 查看顶点 w 是否与起点联通
* @param w 顶点
* @return 联通 true,不连通 false
*/
public boolean marked ( int w ){
return marked [ w ];
}
/**
* 获取与起点联通的结点数
* @return 结点数
*/
public int count (){
return count ;
}
}
多点可达性的一个重要的实际应用是在典型的内存管理系统中,包括许多 Java 的实现。在一幅有向图中,一个顶点表示一个对象,一条边则表示一个对象对另一个对象的引用。这个模型很好地表现了运行中的 Java 程序的内存使用状况。在程序执行的任何时候都有某些对象是可以被直接访问的,而不能通过这些对象访问到的所有对象都应该被回收以便释放内存。
有时候找到一条顶点间的有向路径还不能满足我们的需求,我们希望能找到连接两个顶点有向路径中最短的那一条。 看到最短是不是马上就想到了 广度优先搜索 ,我们只需要给 breadthFirstPaths 添加一个接受有向图参数构造函数和bfs()方法, 方法内容与无向图一模一样。我们就可以找到两个连通顶点间最短的有向路径(由于无向图与有向图的数据表示与无向图没有区别,只是在逻辑上有区别)。构造函数,bfs()函数如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public BreadthFirstPaths ( Digraph g , int s ){
marked = new boolean [ g . V ()];
edgeTo = new int [ g . V ()];
this . s = s ;
bfs ( g , s );
}
/**
* 广度优先搜索函数(使用队列控制搜索元素)
* @param g 有向图
* @param s 起点
*/
private void bfs ( Digraph g , int s ){
Queue < Integer > queue = new ArrayDeque <>();
marked [ s ] = true ;
queue . offer ( s );
while (! queue . isEmpty ()){
int v = queue . poll ();
for ( int w : g . adj ( v )){
if (! marked [ w ]){
edgeTo [ w ] = v ;
marked [ w ] = true ;
queue . offer ( w );
}
}
}
}
4. 环和有向无环图 在和有向图相关的实际应用中,有向环特别的重要。没有计算机的帮助,在一幅普通的有向图中找出有向环可能会很困难。从原则上来说,一幅有向图可能含有大量的环;在实际应用中,我们一般只会重点关注其中一小部分,或者只想知道它们是否存在。
4.1 调度问题 我们经常会碰到这样一个问题:为一组需要完成的任务排好执行顺序序,而且任务间是有依赖关系的,有些任务必须在另一任务完成的前提下才能进行。这个时候我们可以将问题抽象成一幅有向图,每一个任务为一个顶点,有向边为任务间的依赖。例如大学生选修课程的问题,抽象出来的一幅图如下所示:
课程有向图 这时学生就需要根据课程间的依赖关系,确定一个合理的顺序修完课程。这也就是 拓扑排序 的功能
4.2 环的检测 在解决任务的调度问题时,抽象出的有向图是不能有环的。假设出现了一个有3个顶点的环,顶点分别为a,b,c。b 执行前需要 a 执行完,c 执行前又需要 b 执行完,而 a 执行又需要 c 执行完。这在我们这个纬度显然是无法同时满足的。所以我们使用图来解决任务调度排序的问题时,需要先检测抽象出的图是否含有环。如果含有环,那么就说明有些任务的划分是不合理的。
在一幅有向图中,环的数量很有可能时指数级别的。我们检测是否存在环就只需要找出一个就可以了。换句话说就是我们需要确定有向图是一幅有向无环图(DAG)才可以对其进行拓扑排序,完成对任务的排序。
判断图中是否存在环,这是深度优先搜索的拿手本领。基于深度优先搜索的实现的 DirectedCycle 如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public class DirectedCycle {
private boolean [] marked ; // 标记已访问过的顶点
private int [] edgeTo ; // 记录起点到各连通顶点的路径
private List < Integer > cycle ; // 存放发现的有向环的所有顶点
private boolean [] onStack ; // 递归调用的栈上的所有顶点
public DirectedCycle ( Digraph g ){
onStack = new boolean [ g . V ()];
marked = new boolean [ g . V ()];
edgeTo = new int [ g . V ()];
for ( int v = 0 ; v < g . V (); v ++)
if (! marked [ v ]) dfs ( g , v );
}
private void dfs ( Digraph g , int v ){
onStack [ v ] = true ;
marked [ v ] = true ;
for ( int w : g . adj ( v )) {
if ( hasCycle ()) return ;
else if (! marked [ w ]) {
edgeTo [ w ] = v ;
dfs ( g , w );
} else if ( onStack [ w ]) { //发现环,装入环所有顶点
cycle = new ArrayList <>();
for ( int i = v ; i != w ; i = edgeTo [ i ]) {
cycle . add ( i );
}
cycle . add ( w );
cycle . add ( v );
}
}
onStack [ v ] = false ;
}
public boolean hasCycle (){
return cycle != null ;
}
public List < Integer > cycle () {
Collections . reverse ( cycle );
return cycle ;
}
该类为标准的递归 dfs() 方法添加了一个布尔类型的数组 onStack[] 来保存递归调用期间栈上的所有顶点。当它找到一条边 v → w 且 w 在栈中时,它就找到了一个有向环。环上的所有顶点可以通过edgeTo[] 中的链接得到。
4.3 拓扑排序 定义:给定一幅有向图,将所有的顶点排序,使得所有的有向边均从排在前面的元素指向排在后面的元素。
显然根据拓扑排序的定义,我们设计一种算法求出图顶点的拓扑排序,就相当于得到了这些顶点所对应任务的一种合理的排序可能,解决上文提到的任务调度的问题。
我们想要得到一种顶点的顺序,可以使用深度优先搜索访问每一个结点,然后将结点加入队列即可。但是在什么时候将结点加入队列是一个关键问题,它可以决定执行后得到的排序的性质。一般情况下我们关心 3 种顶点的顺序:
前序:在递归访问顶点前加入队列。
后序:在递归访问顶点后加入队列。
逆后序:后序顺序的逆序。(拓扑排序)
基于深度优先搜索的顶点排序类:DepthFirstOrder 如下。实现了 pre(),post(), reversePost()。可以获得基于深度优先遍历图顶点的前序序列,后序序列,逆后序序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public class DepthFirstOrder {
private boolean [] marked ; // 标记已访问过的顶点
private ArrayList < Integer > pre ; // 前序遍历顶点排列
private ArrayList < Integer > post ; // 后序遍历顶点排列
public DepthFirstOrder ( Digraph g ){
pre = new ArrayList <>();
post = new ArrayList <>();
marked = new boolean [ g . V ()];
for ( int s = 0 ; s < g . V (); s ++)
if (! marked [ s ]) dfs ( g , s );
}
/**
* 深度优先搜索函数
* @param g 图
* @param v 当前顶点
*/
private void dfs ( Digraph g , int v ){
pre . add ( v );
marked [ v ] = true ;
for ( int w : g . adj ( v )) {
if (! marked [ w ]) dfs ( g , w );
}
post . add ( v );
}
public List < Integer > pre (){
return pre ;
}
public List < Integer > post () {
return post ;
}
public List < Integer > reversePost (){
Collections . reverse ( post );
return post ;
}
}
在做了上文的有向环检测,有向图顶点排序后,实现拓扑排序就非常简单了。因为拓扑排序使用的就是:基于深度优先搜索遍历顶点的后逆序。我们直接写一个测试用例,以4.1的图为输入,输出其拓扑排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
------------------------------------- 用例输入 -------------------------------------
Algorithms / Theoretical CS / Databases / Scientific Computing
Introduction to CS / Advanced Programming / Algorithms
Advanced Programming / Scientific Computing
Scientific Computing / Computational Biology
Theoretical CS / Computational Biology / Artificial Intelligence
Linear Algebra / Theoretical CS
Calculus / Linear Algebra
Artificial Intelligence / Neural Networks / Robotics / Machine Learning
Machine Learning / Neural Networks
------------------------------------- 用例代码 -------------------------------------
@Test
public void TopologicalTest () throws IOException {
File file = new File ( "src/resources/course.txt" );
InputStream in = new FileInputStream ( file );
BufferedReader reader = new BufferedReader ( new InputStreamReader ( in ));
reader . mark (( int )( file . length ()+ 1 ));
SymbolDigraph digraph = new SymbolDigraph ( reader , "/" );
DirectedCycle cycleFinder = new DirectedCycle ( digraph . getGraph ());
if (! cycleFinder . hasCycle ()) {
DepthFirstOrder dfs = new DepthFirstOrder ( digraph . getGraph ());
List < Integer > topological = dfs . reversePost ();
for ( int v : topological ){
System . out . println ( v + "--" + digraph . name ( v ));
}
}
}
------------------------------------- 用例输出 -------------------------------------
9 -- Calculus
8 -- Linear Algebra
4 -- Introduction to CS
5 -- Advanced Programming
0 -- Algorithms
3 -- Scientific Computing
2 -- Databases
1 -- Theoretical CS
7 -- Artificial Intelligence
12 -- Machine Learning
11 -- Robotics
10 -- Neural Networks
6 -- Computational Biology
在测试用例代码中,首先判断了一下图是否含有环,然后再进行拓扑排序。再实际的其他许多问题上都是需要这样的流程的。
根据用例输出的序列,与4.1图(图中标号根据输入得出)比较发现是满足拓扑排序的条件,所有的有向边均从排在前面的元素指向排在后面的元素。
5. 有向图的强连通性 在术语表中我们提到了有向图的强连通:有向图中两顶点相互可达则称它们为强连通。若图中所有顶点强连通则有向图为强连通有向图。
环与顶点的强连通具有密切联系。 实际上,若有向图的两顶点强连通它们必定会在一个有向环中。 最简单只含两个顶点的图,两顶点强连通就是一个环。其他复杂的情况只是在这个环中增加顶点而已。
5.1 强连通分量 有向图的强连通分量与无向图的连通分量定义类似:有向图的一个强连通分量就是它的一个极大强连通子图。
与连通分量类似,强连通分量的划分也是基于顶点的,而不是基于边。因为有些边会同时属于多个强连通分量。
识别有向图中的强连通分量有什么作用呢?我们计算的图都是由一些实际的问题抽象出来的。如果有向图中几个强连通的顶点构成一个连通分量,哪它们所映射到的事物之间是不是也有某种关联?可以被这种关联划分为一类。这就是强连通分量的作用。
例如,强连通分量能够帮助教科书的作者决定哪些话题应该被归为一类,帮助程序员组织程序的模块,或帮助网络工程师将网络中数量庞大的网页分为多个大小可以接受的部分分别进行处理等等。
5.2 Kosaraju 算法 由于计算有向图的强连通分量有诸多用处,高效的计算出有向图的强连通分量是一个很值得研究的问题。经过先驱的努力,Kosaraju 算法就可以高效的完成任务。
Kosaraju 算法的基本流程为:
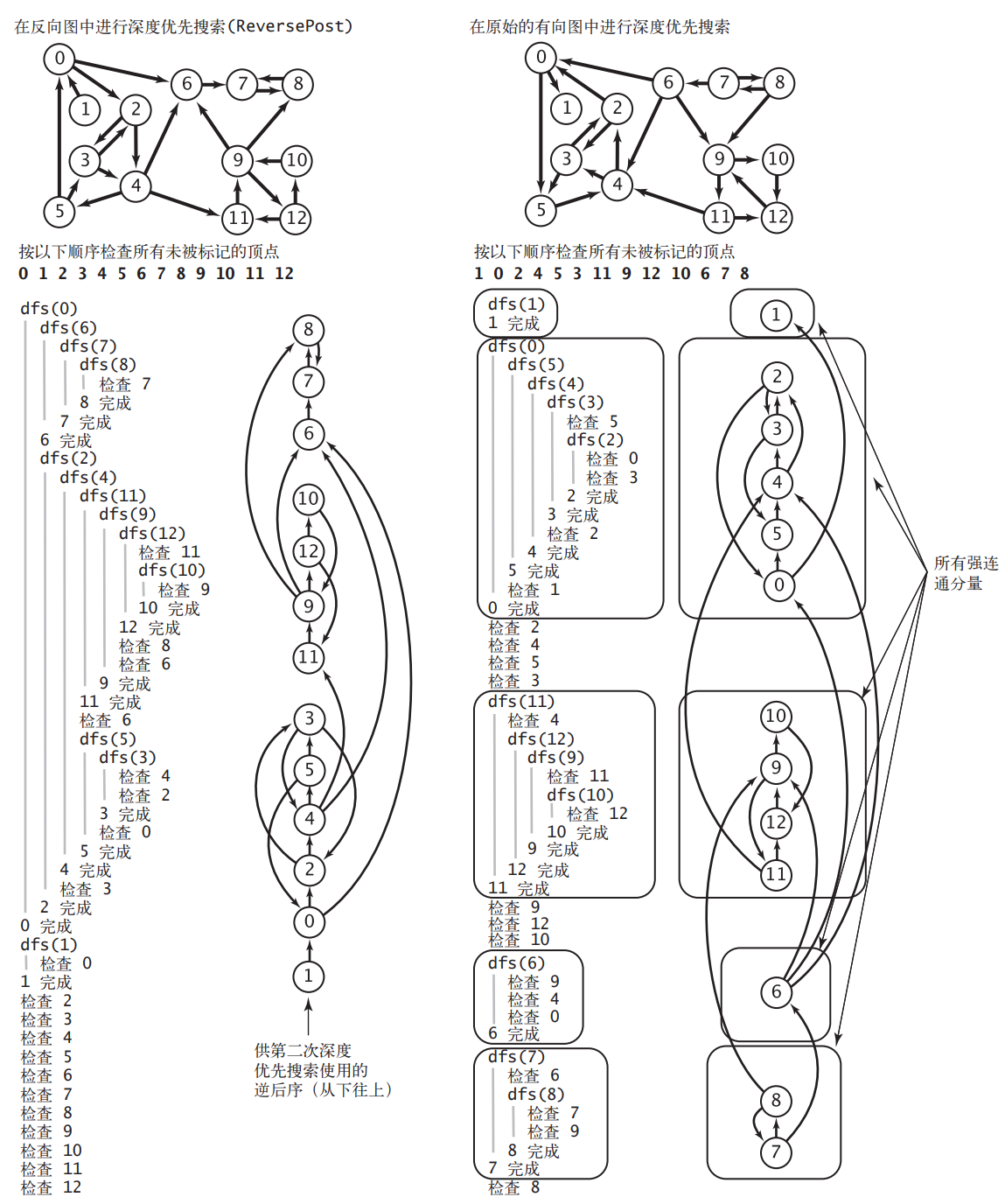
在给定一幅有向图 G 中,计算其反向图 G^R 的拓扑排序(逆后序)。
根据得到的拓扑排序顶点序列,对 G 进行标准的深度优先搜索访问顶点。
在构造函数中,所有在同一个递归 dfs() 调用中被访问到的顶点都在同一个强连通分量中。以发现顺序-1为id记录强连通分量(与无向图连通分量计算的CC类似)
其基本实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class KosarajuSCC {
private boolean [] marked ; // 标记已访问过的顶点
private int [] id ; // 顶点对应索引,值为连通分量的id
private int count ; // 连通分量数
public KosarajuSCC ( Digraph g ){
marked = new boolean [ g . V ()];
id = new int [ g . V ()];
// 使用图的后逆序遍历顶点,以顶点作为起点搜索图
DepthFirstOrder order = new DepthFirstOrder ( g . reverse ());
for ( int s : order . reversePost ()) {
System . out . println ( s );
if (! marked [ s ]) {
dfs ( g , s );
count ++;
}
}
}
private void dfs ( Digraph g , int v ){
marked [ v ] = true ;
id [ v ] = count ;
for ( int w : g . adj ( v ))
if (! marked [ w ]) dfs ( g , w );
}
public boolean stronglyConnected ( int v , int w ){
return id [ v ] == id [ w ];
}
public int id ( int v ){
return id [ v ];
}
public int count (){
return count ;
}
}
Kosaraju 算法的实现很简单,但是其正确性很难直观的看出来。就需要一个严谨的证明去证明其正确性。
证明:
首先要用反证法证明“每个和 s 强连通的顶点 v 都会在构造函数调用的 dfs(G,s) 中被访问到”。假设有一个和 s 强连通的顶点 v 不会在构造函数调用的 dfs(G,s) 中被访问到。因为存在从 s 到 v 的路径,所以 v 肯定在之前就已经被标记过了。但是,因为也存在从 v 到s 的路径,在 dfs(G,v) 调用中 s 肯定会被标记,因此构造函数应该是不会调用 dfs(G,s) 的。矛盾。
从下面这张图可以非常直观的看到 Kosaraju 算法排序的过程。
Kosaraju 运算过程 左边得到反向图 G^R 的拓扑排序,右边根据 G^R 的拓扑排序访问顶点找出所有的强连通分量。
Algorithms (4th Edition) 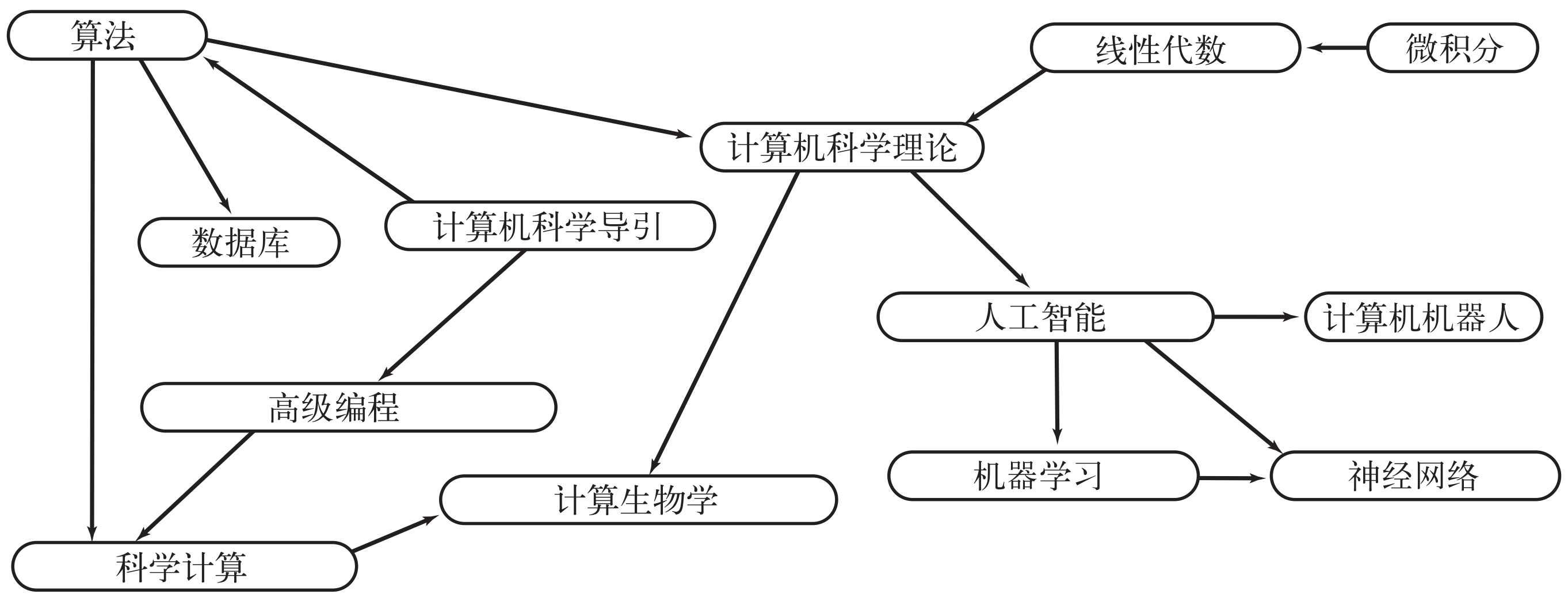
 COMPASSAK
COMPASSAK