Quick-Sort

快速排序算法可能是应用最为广泛的算法，它的实现较为简单而且排序效率比大多数算法都要高。仅需要一个辅助栈就可以实现在原数组上原地排序。但是快速排序算法稳定性不高，如果使用不当经常可能使算法的时间复杂度提升至 O(n^2) 级别。如何正确使用和优化快速排序是使用它之前必须研究的问题。

1. 基本实现

快速排序算法和并归的共性就是它们都是一种分治排序算法，而且在某种意义上，两种算法是互补的。并归是将待排序数组平分（递归的）两个子数组，将两个子数组排序后将结果并归起来就得到了一个有序数组。

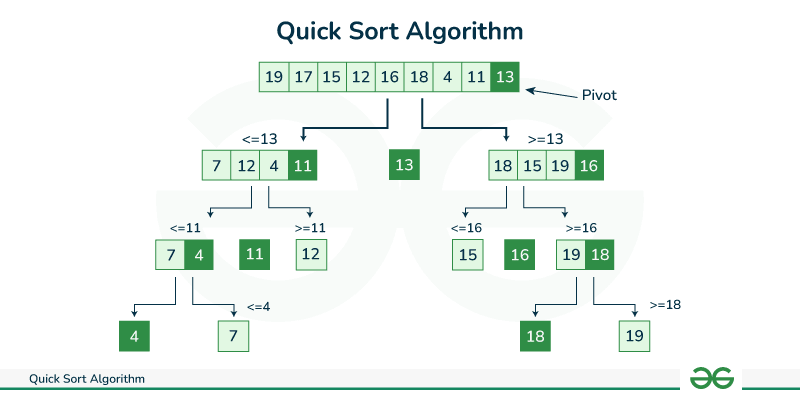
而 快速排序是选取一个切分元素，将数组切分（递归的）为两个子数组，然后将两个子数组分别排序，子数组排序完成整个数组也就排好序了。

这一区别在代码中的体现就是并归排序的递归调用发生在处理整个数组之前，在快速排序中，递归调用发生在处理整个数组之后。快速排序基本实现如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

public class Quick {
    public static void sort(int[] a){
        sort(a, 0, a.length - 1);
    }

    private static void sort(int[] a, int lo, int hi){
        if(hi <= lo)return;
        int j = partition(a, lo, hi);
        sort(a, lo, j-1);
        sort(a, j+1, hi);
    }

    //切分操作
    private static int partition(int[] a, int lo, int hi){
        //左右扫描指针
        int i = lo, j = hi+1;
        //切分元素
        int V = a[lo];
        while (true){
            //扫描左右元素，出现左元素比V大或右元素比V小，则交换两元素位置。
            while (a[++i] < V) if (i == hi) break;
            while (a[--j] > V) if (j == lo) break;
            if (i >= j) break;
            exch(a, i, j);
        }
        exch(a, lo, j);
        return j;
    }

    //交换元素位置
    private static void exch(int[] a, int i, int j){
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }
}

此算法实现的关键在于切分如何实现，在上述代码中切分操作的实现思路为：

1. 首先选取数组第一个元素为切分元素。
2. 从左到右，从右到左的扫描数组，出现左元素比V大或右元素比V小，则交换两元素位置。
3. 直到整个数组被扫描一遍后，切分完成。此时切分元素左的边元素都小于等于它，切分元素右边的元素都大于等于它，最后返回切分元素所在位置的索引。

2. 性能特点

快速排序切分方法的内循环会用一个递增的索引将数组元素和一个定值比较。这种简洁性也是快速排序的一个优点。归并排序和希尔排序一般都比快速排序慢，其原因就是它们还在内循环中移动数据。

快速排序另一个速度优势在于它的比较次数很少。排序效率最终还是依赖切分数组的效果， 而 这依赖于切分元素的值。这就是让快速排序算法不稳定的因素。快速排序的最好情况是每次都正好能将数组对半分。在这种情况下快速排序所用的比较次数正好满足分治递归的 CN=2CN/2+N 公式。 在前面属于分治递归的并归排序的算法时间复杂度证明得到此公式的解为：CN~NlgN。

但是在使用是不可能每次都能有这样的好运气，所以我们需要在数学上证明一下其平均的时间复杂度，以便于更好的了解使用它。

命题 K 将长度为 N 的无重复数组排序，快速排序平均需要 ~2NlnN 次比较（以及 1/6 的交换）

1. 令 CN 为将 N 个不同元素排序平均所需的比较次数。显然 C0=C1=0，对于 N>1，由递归 程序可以得到以下归纳关系：

   CN = N+1+(C0+C1+…+CN-2+CN-1)/N+(CN-1+CN-2+…+C0)/N

   第一项是切分的成本（总是 N+1），第二项是将左子数组（长度可能是 0 到 N-1）排序的平均成本，第三项是将右子数组（长度和左子数组相同）排序的平均成本。

2. 将等式左右两边乘以N并整理各项得到：

   NCN = N(N+1)+2(C0+C1+…+CN-2+CN-1)

3. 将该等式减去 N-1 时的相同等式可得：

   NCN-(N-1)CN-1 = 2N+2CN-1

4. 整理等式并将两边除以 N(N+1) 可得：

   CN/(N+1) = CN-1/N+2/(N+1)

5. 归纳法推导可得：

   CN~2(N+1)(1/3+1/4+…+1/(N+1))

   括号内的量是曲线 2/x 下从 3 到 N 的离散近似面积加一， 积分得到 CN~2NlnN。 注意到 2NlnN ≈ 1.39NlgN，也就是说平均比较次数只比最好情况多 39%。 要得到命题中的交换次数需要一个类似（但更加复杂的）分析。

总的来说，可以肯定的是对于大小为 N 的数组,上述的快速排序算法的运行时间在 1.39NlgN 的某个常数因子的范围之内。归并排序也能做到这一点，但是快速排序一般会更快（尽管它的比较次数多39%），因为它移动数据的次数更少。

3. 算法改进

实际应用中经常会出现含有大量重复元素的数组，一个元素全部重复的子数组就不需要继续排序了，但我们的算法还会继续将它切分为更小的数组。在有大量重复元素的情况下，快速排序的递归性会使元素全部重复的子数组经常出现，这就有很大的改进潜力，将当前实现的线性对数级的性能提高到线性级别。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

public class Quick3way {
    public static void sort(int[] a){
        sort(a, 0, a.length - 1);
    }

    private static void sort(int[] a, int lo, int hi){
        if (hi <= lo) return;
        int lt = lo, i = lo+1, gt = hi;
        int v = a[lo];
        while (i <= gt)
        {
            if (a[i] < v) exch(a, lt++, i++);
            else if (a[i] > v) exch(a, i, gt--);
            else i++;
        }
        // 现在 a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi]成立
        sort(a, lo, lt - 1);
        sort(a, gt + 1, hi);
    }

    //交换元素位置
    private static void exch(int[] a, int i, int j){
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }
}

Dijkstra 的解法如上所示。它从左到右遍历数组一次，维护一个指针 lt 使得 a[lo..lt-1] 中的元素都小于 v，一个指针 gt 使得 a[gt+1..hi] 中的元素都大于 v，一个指针 i 使得 a[lt..i-1] 中的元素都等于 v， a[i..gt] 中的元素都还未确定。直到while循环完成后，就达到了a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi]成立的效果。 对于存在大量重复元素的数组，这种方法比标准的快速排序的效率高得多

图片资料来自：

1. Algorithms (4th Edition)

2. GeeksforGeeks