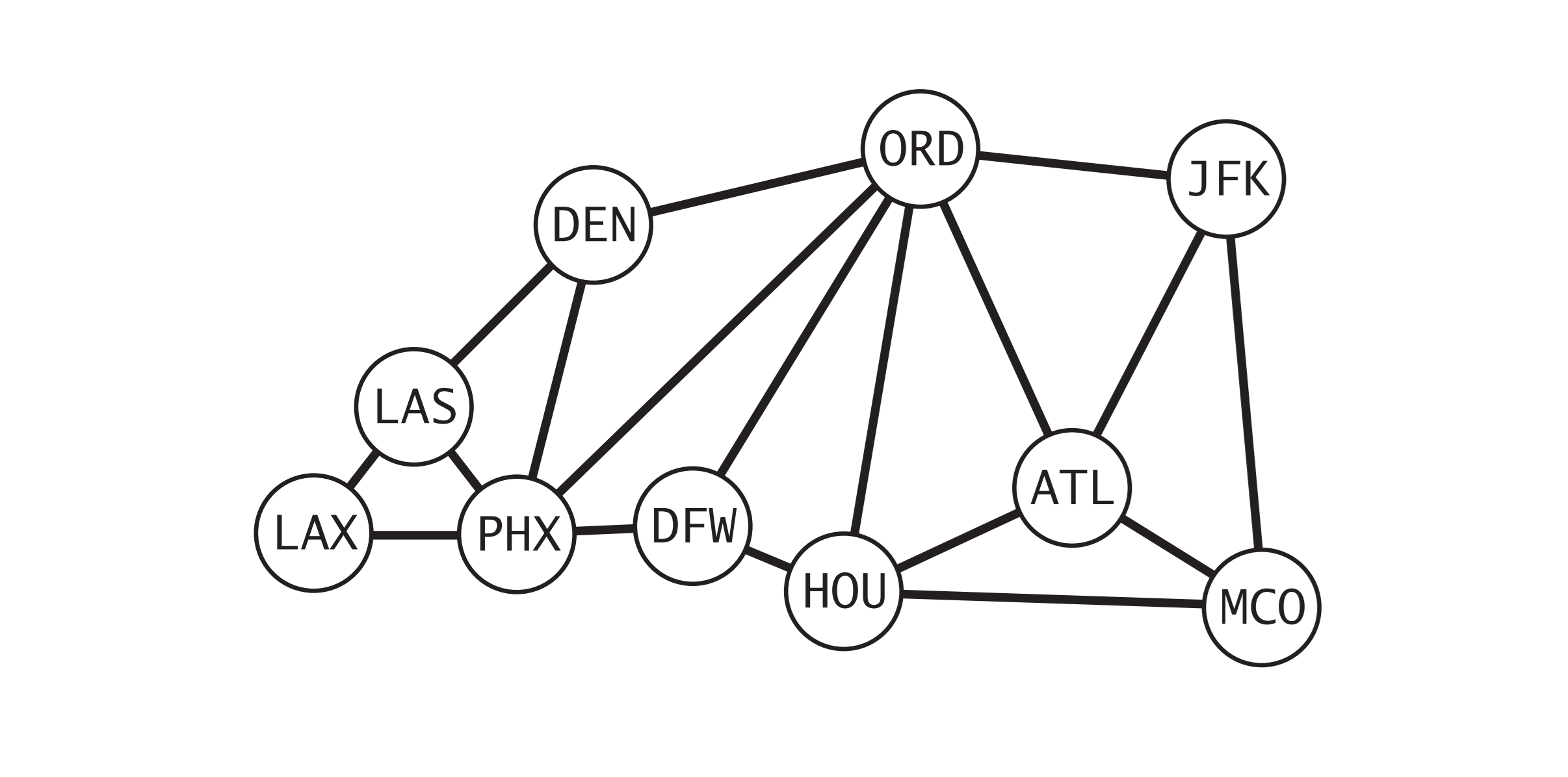
图是由一组顶点和一组能够将两个顶点相连的边组成的逻辑结构，一般情况下为了和其他的图模型相互区别，又称图为无向图。在现实中的许多问题都可以抽象为一张图，结合优秀的算法，许多困难的问题都可以迎刃而解。
1. 术语表
和图有关的术语，定义非常多，其一部分内容如下：
| 术语 | 条件（释义） |
|---|
| 顶点相邻 | 两个顶点通过一条边相连时，并称这条边 依附于 这两个顶点 |
| 顶点的度数 | 连接它边的总数 |
| 子图 | 指定图的子集 |
| 路径 | 由边顺序连接的一系列顶点 |
| 简单路径 | 一条没有重复顶点的路径 |
| 环 | 含有至少一条边且起点和终点相同的路径 |
| 简单环 | 除起点和终点相同外，不含有重复顶点和边的环 |
| 顶点连通 | 两个顶点间存在一条连接双方的路径时 |
| 连通图 | 图中任意一个顶点都存在一条路径到达另外一个顶点 |
| 极大连通子图 | 非连通图的一个连通部分 |
| 无环图 | 不包含环的图 |
| 图密度 | 指已经连接的顶点对占所有可能被连接顶点对的比例 |
| 稀疏图 | 很少的顶点对被连接 |
| 稠密图 | 很少的顶点对没有被连接 |
| 二分图 | 顶点可分割为两个互不相交的子集，两个子集内的顶点不相邻 |
2. 表示无向图数据类型
2.1 图的几种表示方法
图的表示方法主要有以下3种：
邻接矩阵：使用一个长宽等于顶点数的布尔矩阵来表示图，当顶点 v 与顶点 w 之间有相连的边时，置 v 行 w 列的元素值为true，否则为false。由于现实的问题抽象出的往往是顶点数非常大的稀疏图，使用这种方法表示图会浪费掉大量资源.
边的数组：使用一个 Edge 类，含两个 int 实例变量。这种方法的缺点是无法快速的找到一个顶点相邻的顶点。
邻接表：使用一个以顶点为索引的列表数组，数组中每一个索引位置元素都是和对应顶点的所有相邻顶点构成的链表。与 基于拉链法的哈希表 逻辑结构类似。这种方法表示图既不会浪费很多资源，又可以非常快的查询到一个与顶点相邻的所有顶点。
2.2 邻接表的表示
前面描述了邻接表的逻辑结构，实现它就很简单了。只需要声明一个静态内部结点类作为以顶点为索引的数组中的元素，结点有顶点号以及指向下一个元素的引用，这样就可以通过数组直接访问到一条条邻接顶点链表。
2.3 实现
声明一个 Node 数组作为邻接表，在两个构造函数中完成对图的初始化，使用reader初始化图时，读取的文件头两行应为顶点数和边数。在添加一条边时，需要在两个顶点的邻接表中都加上对方的顶点结点。这样方便我们在实现 adj() 方法时可以简单高效的找出一个顶点的所有邻接顶点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| public class Graph {
private final int V; // 顶点数
private int E; // 边数
private Node[] adj; // 邻接表
/**
* 邻接表结点静态内部类
*/
private static class Node{
int vertex; // 顶点
Node next; // 下一个元素的引用
Node(){}
Node(int vertex, Node next){
this.vertex = vertex;
this.next = next;
}
}
public Graph(int V){
this.V = V;
this.E = 0;
this.adj = new Node[V]; // 创建邻接表
}
public Graph(BufferedReader reader) throws IOException {
this(Integer.parseInt(reader.readLine())); // 读取 V
int E = Integer.parseInt(reader.readLine()); // 读取 E
for (int i = 0; i < E; i ++){
String str = reader.readLine();
String[] edge= str.split(" ");
int v = Integer.parseInt(edge[0]);
int w = Integer.parseInt(edge[1]);
addEdge(v, w); // 添加边
}
}
/**
* 添加一条边
* @param v 顶点1
* @param w 顶点2
*/
public void addEdge(int v, int w){
Node first = adj[v];
adj[v] = new Node(w, first); // 将w添加到v的链表中
first = adj[w];
adj[w] = new Node(v, first); // 将v添加到w的链表中
E++;
}
/**
* 获取与顶点 v 邻接的所有顶点
* @param v 顶点
* @return 邻接顶点set集合
*/
public Set<Integer> adj(int v){
Node node = adj[v];
Set<Integer> set = new HashSet<>();
while (node != null){
set.add(node.vertex);
node = node.next;
}
return set;
}
public int V(){ return V;}
public int E(){ return E;}
}
|
在上面的实现中，可能几个不同的邻接表对应同一幅图，这与边插入的顺序有关。而且在最后调用方法 adj() 获取所有邻接顶点时，使用的是 HashSet 存储顶点元素又会将元素的顺序打乱（按在HashSet中的存储位置顺序），此时元素的顺序就是算法处理它们的顺序。虽然顺序的差异不会对算法的正确性有影响。
3. 深度优先搜索
深度优先搜索（DFS）是一种遍历连通图的算法，它算法的基本思路为：
从一个指定的顶点（起点）开始遍历。
将访问过的顶点标记为已访问。
递归的访问当前顶点所有没有被标记过的邻接顶点。
深度优先搜索可以通俗的理解为一条道走到黑遍历算法，首先它会访问起点的第一个邻接顶点，然后又会访问第一个邻接顶点的第一个邻接顶点。如此递归下去，当到访问到一个已经被访问的顶点，往后退一步继续递归访问，直到所有与起点连通的顶点都被访问过后，算法结束。
可以说是非常的头铁了，给人一种到处乱串的感觉，一直走到相对于起点的最深处才罢休。它的基本实现如下（基于 Graph 数据类型）。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| public class DepthFirstSearch {
private boolean[] marked; // 标记已访问过的顶点
private int count; // 与起点连通的结点数
public DepthFirstSearch(Graph g, int s){
marked = new boolean[g.V()];
dfs(g, s);
}
/**
* 深度优先搜索函数
* @param g 图
* @param v 当前顶点
*/
private void dfs(Graph g, int v){
marked[v] = true;
count++;
for (int w : g.adj(v))
if (!marked[w]) dfs(g, w);
}
/**
* 查看顶点 w 是否与起点联通
* @param w 顶点
* @return 联通 true，不连通 false
*/
public boolean marked(int w){
return marked[w];
}
/**
* 获取与起点联通的结点数
* @return 结点数
*/
public int count(){
return count;
}
}
|
有了深度优先搜索我们可以解决很多图的问题：
计算一幅图的极大连通子图数(连通分量)
确定两个顶点是否连通（两个顶点间是否存在一条路径）
判断一幅图是否存在环
判断一幅图是不是二分图
等等，图论中的许多问题都可以使用深度优先搜索来解决。只需要在经典的深度优先搜索上稍加修改（记录一下数据）即可。
3.1 连通分量
图的连通分量也就是图的极大连通子图。基于深度优先搜索计算一幅图的连通分量数的思路是：利用深度优先搜索每次都会遍历完一个包含起点的连通图的性质。将每一个顶点都轮流作为起点，找到一幅连通子图计数器加一。
在CC的实现中，使用一个int数组 id 来存储每一个顶点的连通分量id（初始化时对应的count），顶点号为数组索引，数组值为连通分量的id。根据id数组我们可以很快的确定两个顶点是否在一个连通分量中（是否连通，之间有路径）。每找到一个连通分量 count加1。具体实现如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| public class CC {
private boolean[] marked; // 标记已访问过的顶点
private int[] id; // 顶点对应索引，值为连通分量的id
private int count; // 连通分量数
public CC(Graph g){
marked = new boolean[g.V()];
id = new int[g.V()];
for (int s = 0; s < g.V(); s++){
if (!marked[s]){
dfs(g, s);
count++;
}
}
}
/**
* 深度优先搜索函数
* @param g 图
* @param v 当前顶点
*/
private void dfs(Graph g, int v){
marked[v] = true;
id[v] = count;
for (int w : g.adj(v))
if (!marked[w]) dfs(g, w);
}
public boolean connected(int v, int w){
return id[v] == id[w];
}
public int id(int v){
return id[v];
}
public int count(){
return count;
}
}
|
3.2 判断环
基于深度优先搜索检测图中是否含有环的基本思路为：在有顶点的边指向已标记的顶点，且已标记顶点不是当前顶点的父顶点时，判定图出现环。这里的父顶点是根据访问顺序来确定，也就是当前顶点前一个被访问的顶点。
在 Cycle 的实现中，增加了 dfs() 的参数 int u，也就是参数int v 的父顶点用于环判定。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| /**
* 判断图中是否有环，假设不存在自环，平行环
*/
public class Cycle {
private boolean[] marked; // 标记已访问过的顶点
private boolean hasCycle; // 是否含有环
public Cycle(Graph g){
marked = new boolean[g.V()];
for (int s = 0; s < g.V(); s++)
if (!marked[s])
dfs(g, s, s);
}
/**
* 深度优先搜索函数（在有顶点的边指向已标记的顶点，且已标记顶点不是当前顶点的父顶点时，判定图出现环）
* @param g 图
* @param v 当前顶点
* @param u 上一个访问的顶点（v的父顶点）
*/
private void dfs(Graph g, int v, int u){
marked[v] = true;
for (int w : g.adj(v))
if (!marked[w])
dfs(g, w, v);
else if (w != u)
hasCycle = true;
}
public boolean HasCycle(){
return hasCycle;
}
}
|
3.3 判断图是否为二分图
二分图的定义在术语表中提到过：顶点可分割为两个互不相交的子集，两个子集内的顶点不相邻。也就是说需要每一条边连接的两个顶点是不同的颜色，所有顶点又分别属于两种颜色。
基于深度优先搜索判断二分图的思路为：这个问题正向证明不是很容易，我们使用反证法。使用深度优先遍历整幅图，在遍历的过程中按二分图定义给顶点上色。如果访问到一个已上色的顶点且其颜色与父顶点相同那么此图就无法构成一个二分图。
在 TowColor 的实现中，使用一个int[] 的 color 记录每一个顶点的颜色。isTowColorable 默认为 true，遇到无法构成2分图的情况置为 false。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public class TowColor {
private boolean[] marked; // 标记已访问过的顶点
private boolean[] color; // 顶点颜色
private boolean isTowColorable = true; // 当前图是否可以构成二分图
public TowColor(Graph g){
marked = new boolean[g.V()];
color = new boolean[g.V()];
for (int s = 0; s < g.V(); s++)
if (!marked[s])
dfs(g, s);
}
/**
* 深度优先搜索函数（如果当前顶点的一条边指向被一个访问过的顶点，且二者颜色一致，则无法构成二分图）
* @param g 图
* @param v 当前顶点
*/
private void dfs(Graph g, int v){
marked[v] = true;
for (int w : g.adj(v)){
if (!marked[w]){
color[w] = !color[v];
dfs(g, w);
}else if (color[w] == color[v])
isTowColorable = false;
}
}
public boolean isTowColorable() {
return isTowColorable;
}
}
|
3.4 寻找路径
判断两个顶点间是否有一条路径的问题在图的处理领域中十分重要的。使用深度优先搜索，我们可以较为简单的实现它。
在DepthFirstPaths的实现中，基于DepthFirstSreach增加了 edgeTo[] 记录起点到各连通顶点的路径，它可以记录每一个顶点到起点的路径。为了做到这一点，在由边 v-w 第一次访问任意 w 时，将 edgeTo[w] 设为 v 来记住这条路径。edgeTo[v] 中又记录了上一个顶点，一直可以回溯到起点。这样在edgeTo[]中存储的就是一个以起点为根结点的树。通过连通的目标顶点我们总能找到一条指向起点的路径。具体实现如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| public class DepthFirstPaths {
private boolean[] marked; // 标记已访问过的顶点
private int[] edgeTo; // 记录起点到各连通顶点的路径
private final int s; // 起点
public DepthFirstPaths(Graph g, int s){
marked = new boolean[g.V()];
edgeTo = new int[g.V()];
this.s = s;
dfs(g, s);
}
/**
* 深度优先搜索函数
* @param g 图
* @param v 当前顶点
*/
private void dfs(Graph g, int v){
marked[v] = true;
for (int w : g.adj(v)){
if (!marked[w]){
edgeTo[w] = v;
dfs(g, w);
}
}
}
/**
* 查看顶点 v 是否与起点联通
* @param v 顶点
* @return 联通 true，不连通 false
*/
public boolean hasPathTo(int v){
return marked[v];
}
/**
* 若顶点 v 与起点联通，获取路径上的结点
* @param v 当前顶点
* @return 表示顶点路径的list集合
*/
public List<Integer> pathTo(int v)
{
if (!hasPathTo(v)) return null;
List<Integer> path = new ArrayList<>();
for (int x = v; x != s; x = edgeTo[x])
path.add(x);
path.add(s);
return path;
}
}
|
测试用例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| 用例输入------------------------------------------------------------
13
13
0 5
4 3
0 1
9 12
6 4
5 4
0 2
11 12
9 10
0 6
7 8
9 11
5 3
用例代码------------------------------------------------------------
int s = 0, v = 6;
//dfp test
DepthFirstPaths dfp = new DepthFirstPaths(graph, s);
List<Integer> path1= dfp.pathTo(v);
System.out.print("dfp "+s+"->"+ v + " : " + s);
for (int i = path1.size()-2; i >= 0; i--){
System.out.print("-" + path1.get(i));
}
用例输出------------------------------------------------------------
dfp 0->6 : 0-5-3-4-6
|
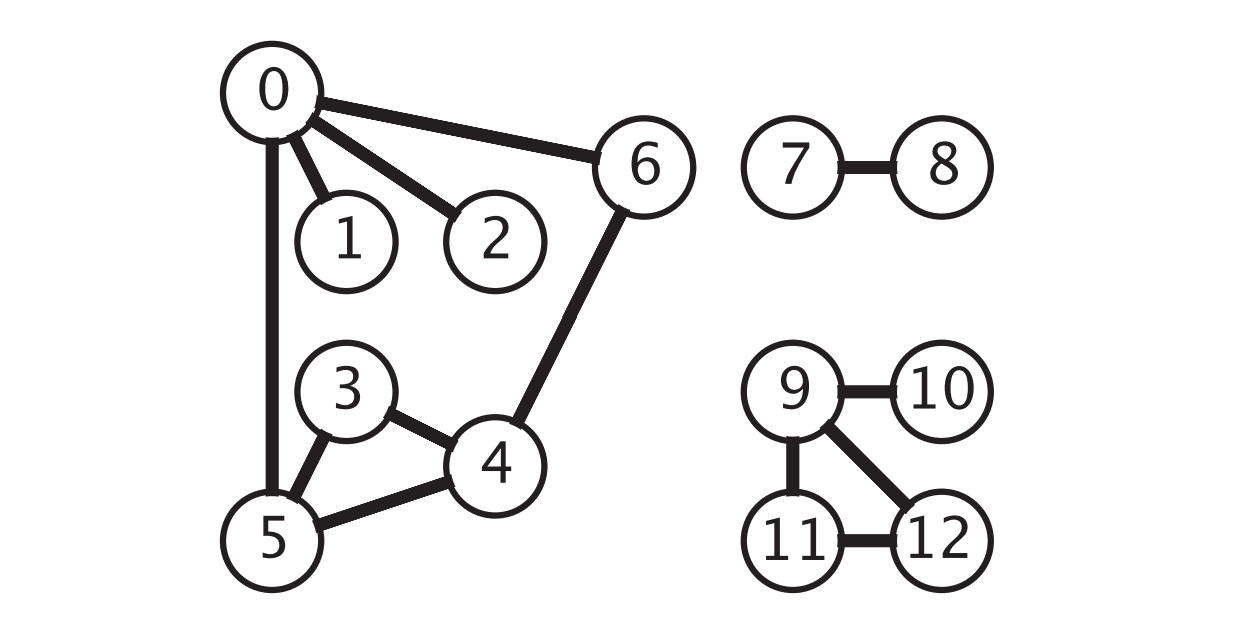深度优先搜索测试用例直接看测试用例输入输出难以验证程序的正确性，根据上图我们可以观察到，使用 DepthFirstPaths 找到的顶点 0->6的路径: 0-5-3-4-6确实存在，程序是正确的。
但是仔细观察，我们会发现找顶点 0->6的路径，可以直接可以从0到6啊？上文提到过，深度优先算法访问顶点的顺序是根据 Graph 的 adj() 方法返回的顶点顺序来的，然后在次用例中可能 5 比 6 先返回。导致绕了一大圈才找到6。
而且上述要求对于深度优先算法太为苛刻，本来就没有这方面的功能属性。要解决这个问题也就是：单点最短路径问题（给定顶点到起点的最短路径）。需要使用另一个经典算法 广度优先搜索 。
4. 广度优先搜索
广度优先搜索（BFS）正是为了解决 单点最短路径问题 才被学者研究出来。它可以容易的找到连通顶点间的最短路径，这对使用图处理现实中的诸多问题起到了非常重大的作用。
在程序中，搜索一幅图时遇到有多条边需要遍历的情况时，我们会选择其中一条并将其他通道留到以后再继续搜索。
在深度优先搜索中，使用的是下压栈（方法递归）来放置还没有处理的边，当我们选取下一条边时自然是根据LIFO（先进后出）的规则取，取到的自然是最晚遇到的那一条边。这样就会一直往图的深处访问。
而在广度优先搜索中我们想要找到顶点到起点的最短路径，就必须对取下一条边的规则重新定义。广度优先搜索是按照顶点到起点的距离来遍历顶点的，也就是说，首先遍历到起点距离为 1 的所有顶点，然后遍历到起点所有距离为 2 的所有顶点以此类推。这样就需要我们在选择下一条边处理时，选择最早遇到的那条边，而不是直接一直往图深处访问。这个顺序规则对应的就是 FIFO（先进先出）规则，实现FIFO我们只需要将遇到的边加入 队列 然后一条条取就行了。
所以广度优先搜索，和深度优先搜索的区别就在于取下一条边的顺序规则。
4.1 实现
BreadthFirstPaths 与 DepthFirstPaths 都使用一个int[] edgeTo 来存储路径，除了控制边访问顺序的代码不同，其余代码几乎都是相同的。
BreadthFirstPaths 的 bfs() 方法中使用了一个 Queue 队列来存放遇到的边。 首先会将起点加入队列，然后重复以下步骤直到队列为空：
取队列中的下一个顶点 v 并标记它；
将与 v 相邻的所有未被标记过的顶点加入队列。
由于需要处理的边都存放在了队列，bfs() 方法就不需要使用递归来处理访问。BreadthFirstPaths 的具体实现如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| public class BreadthFirstPaths {
private boolean[] marked; // 到达该顶点的最短路径是否已知
private int[] edgeTo; // 记录起点到各连通结点的最短路径
private final int s; // 起点
public BreadthFirstPaths(Graph g, int s){
marked = new boolean[g.V()];
edgeTo = new int[g.V()];
this.s = s;
bfs(g, s);
}
/**
* 广度优先搜索函数（使用队列控制搜索元素）
* @param g 图
* @param s 起点
*/
private void bfs(Graph g, int s){
Queue<Integer> queue = new ArrayDeque<>();
marked [s] = true;
queue.offer(s);
while (!queue.isEmpty()){
int v = queue.poll();
for (int w : g.adj(v)){
if (!marked[w]){
edgeTo[w] = v;
marked[w] = true;
queue.offer(w);
}
}
}
}
/**
* 查看当前顶点 v 是否与起点连通
* @param v 当前顶点
* @return 连通 true，不连通
*/
public boolean hasPathTo(int v){
return marked[v];
}
/**
* 若顶点 v 与起点联通，获取路径上的结点
* @param v 当前顶点
* @return 表示顶点路径的list集合
*/
public List<Integer> pathTo(int v)
{
if (!hasPathTo(v)) return null;
List<Integer> path = new ArrayList<>();
for (int x = v; x != s; x = edgeTo[x])
path.add(x);
path.add(s);
return path;
}
}
|
测试用例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| 用例输入------------------------------------------------------------
与 3.4 节一致
用例代码------------------------------------------------------------
int s = 0, v = 6;
//bfp test
BreadthFirstPaths bfp = new BreadthFirstPaths(graph, s);
List<Integer> path2 = bfp.pathTo(v);
System.out.print("bfp "+s+"->"+ v + " : " + s);
for (int i = path2.size()-2; i >= 0; i--){
System.out.print("-" + path2.get(i));
}
用例输出------------------------------------------------------------
bfp 0->6 : 0-6
|
我们从输出可以看见，广度优先搜索选择了最短最优的路径，从0直接到6。
广度优先搜索与深度优先搜索的区别从下图中可以更明显的看出：
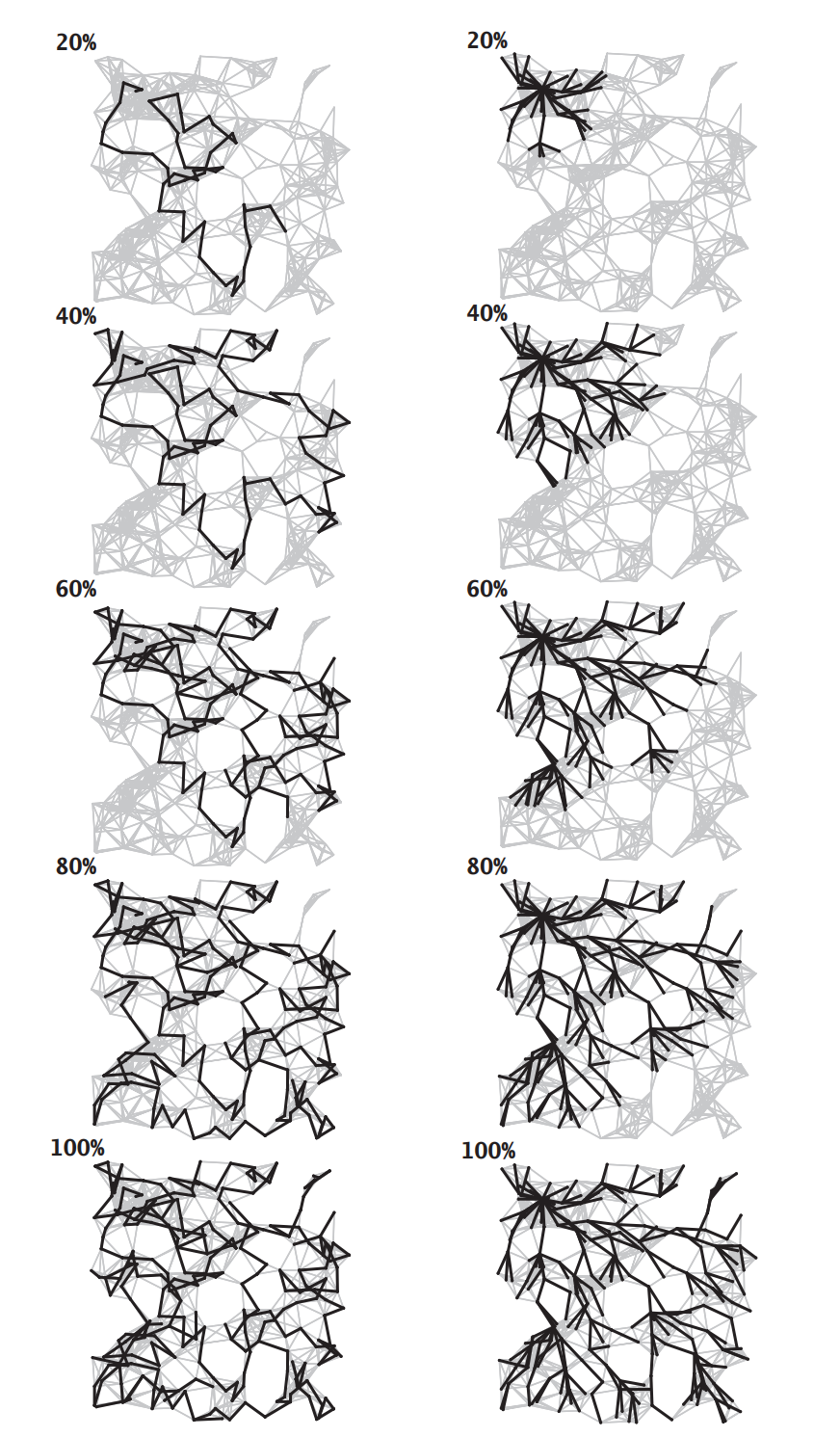深度优先和广度优先区别上图，显示了深度优先搜索和广度优先搜索处理含有250个顶点图的过程，左图为深度优先搜索，右图为广度优先搜索，它们清晰地展示了两种方法中搜索路径的不同。深度优先搜索不断深入图中并在栈中保存了所有分叉的顶点；广度优先搜索则像扇面一般扫描图，用一个队列保存访问过的最前端的顶点。深度优先搜索探索一幅图的方式是寻找离起点更远的顶点，只在碰到死胡同时才访问近处的顶点；广度优先搜索则会首先覆盖起点附近的顶点，只在临近的所有顶点都被访问了之后才向前进。
5. 符号图
在图算法实际的应用中，处理的很多问题是从现实的问题中抽象出一幅图。图的顶点往往是用字符串代指的。而且不会像 Graph 接受的输入会预先告知顶点数边数。为了用图的算法去更好的处理实际问题，我们需要将使用数字顶点的图Graph 数据类型扩展成字符串代指顶点的图，而且会根据输入来自动确定定点数，边数。
在 SymbolGraph 符号图的实现中，使用 Graph 作为基础数据类型，使用一个符号表 HashMap 完成顶点字符串到顶点号的映射。使用一个 String[] 对应着HashMap 的反向索引，以顶点号作为索引，值为顶点名。有了着两个符号表我们可以轻松的根据顶点名得到顶点号，或者根据顶点号知道顶点名。
HashMap 正向索引值为上一次元素添加后 HashMap 的元素数量。SymbolGraph 符号图的具体实现如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| public class SymbolGraph {
private HashMap<String, Integer> map; // 符号名 -> 索引
private String[] keys; // 索引 -> 符号名
private Graph graph; // 图
public SymbolGraph(BufferedReader reader, String sp) throws IOException {
map = new HashMap<>();
String temp;
// 初始化符号表，生成正向索引
while ((temp = reader.readLine()) != null) {
String[] vertex = temp.split(sp);
for (String s : vertex) {
if (!map.containsKey(s))
map.put(s, map.size());
}
}
// 初始化反向索引
keys = new String[map.size()];
for (String name : map.keySet()) {
keys[map.get(name)] = name;
}
graph = new Graph(map.size());
reader.reset();
// 添加边
while ((temp = reader.readLine()) != null) {
String[] vertex = temp.split(sp);
int v = map.get(vertex[0]);
for (int i = 1; i < vertex.length; i++)
graph.addEdge(v, map.get(vertex[i]));
}
}
public boolean contains(String s){
return map.containsKey(s);
}
public int index(String s){
return map.get(s);
}
public String name(int v) {
return keys[v];
}
public Graph getGraph(){
return graph;
}
}
|
测试用例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| 用例输入------------------------------------------------------------
JFK MCO
ORD DEN
ORD HOU
DFW PHX
JFK ATL
ORD DFW
ORD PHX
ATL HOU
DEN PHX
PHX LAX
JFK ORD
DEN LAS
DFW HOU
ORD ATL
LAS LAX
ATL MCO
HOU MCO
LAS PHX
用例代码
------------------------------------------------------------
File file = new File("src/resources/route.txt");
InputStream in = new FileInputStream(file);
BufferedReader reader = new BufferedReader(new InputStreamReader(in));
reader.mark((int)(file.length()+1));
SymbolGraph graph = new SymbolGraph(reader, " ");
System.out.println(graph.index("PHX"));
System.out.println(graph.name(6) + "\n----------------------------------------------");
String s = "JFK", v = "LAS";
//dfp test
DepthFirstPaths dfp = new DepthFirstPaths(graph.getGraph(), graph.index(s));
List<Integer> path1= dfp.pathTo(graph.index(v));
System.out.print("dfp "+ s +"->"+ v + " : " + s);
for (int i = path1.size()-2; i >= 0; i--){
System.out.print("-" + graph.name(path1.get(i)));
}
//bfp test
BreadthFirstPaths bfp = new BreadthFirstPaths(graph.getGraph(), graph.index(s));
List<Integer> path2 = bfp.pathTo(graph.index(v));
System.out.print("\nbfp "+ s +"->"+ v + " : " + s);
for (int i = path2.size()-2; i >= 0; i--){
System.out.print("-" + graph.name(path2.get(i)));
}
用例输出------------------------------------------------------------
6
PHX
----------------------------------------------
dfp JFK->LAS : JFK-MCO-HOU-ORD-DEN-PHX-LAX-LAS
bfp JFK->LAS : JFK-ORD-DEN-LAS
|
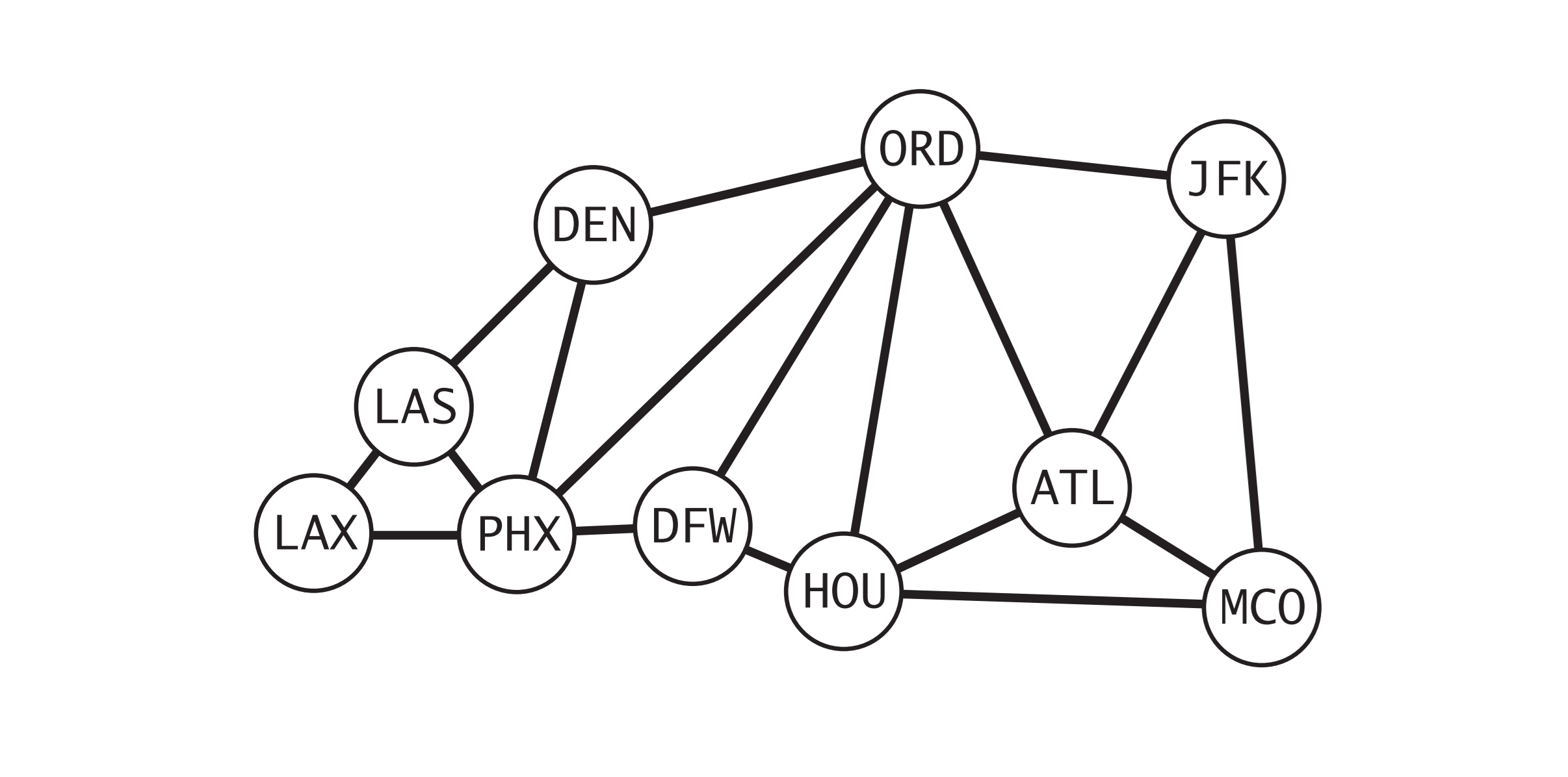美国机场航线图上述用例输入的是根据一个小运输系统抽象出来的模型，具体的情况如上图所示。其中表示每个顶点的是美国机场的代码，连接它们的边则表示顶点之间的
航线。用例输入只有边而没有顶点数，边数。在用例代码中表示顶点也可以使用字符串来表示，更方便处理实际问题。
根据虚线上的输出可以发现正向索引与反向索引对应良好。在虚线输出后分别使用了深度优先搜索，广度优先搜索，查询 JFK -> LAS 间的路径。深度优先搜索还是一如既往的头铁，找出了一条非常长的路径。而广度优先搜索则是不负众望找到了一条通过定点数最少的路径之一。
图片资料来自：
- Algorithms (4th Edition)
COMPASSAK